держки которого равно tvt при условии W{0)=R. Условия реализуемости линии:

-<1 или /?С>/з = ~-

Максимальное значение выходного напряжения может быть получено при

з = /?СилиС = .

В качестве сопротивления R может быть использовано выходное сопротивление питающего схему источника.

В том случае если длительность fn импульса превосходит несколько сотен наносекунд, отрезок линии удобно заменить эквивалентной ему по входному сопротивлению схемой, состоящей из последовательно соединенных параллельных контуров (см. рис, 5-74). Если параметры входящих в схему контуров рассчитаны по формулам (5-45), то его входное сопротивление, измеренное точками ас/, равно:

а следовательно, сопротивление между точками аЬ определяется выражением

Zab(p) = Rcih--.

а емкость конденсатора С оказывается равной ta/2R. Таким образом, схема оптимального фильтра принимает вид, приведенный иа рис. 5-86.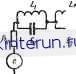

Рис. 5-86. Схема оптимального фильтра с эквивалентом отрезка параболической линии.

Опыт показывает, что для того чтобы получить достаточно хорошее с практической точки зрения приближение к оптимальному фильтру, достаточно включить в приведенную схему три-четыре параллельных контура.

Пусть фильтруемый сигнал представляет собой прямоугольный радиоимпульс и аналитически описывается выражением

u{f)=E [cos (Оо tl (t) - cos (Оо {t - tu) X

Xl{t-t)].

Будем считать, что в импульсе укладывается целое число периодов высокочастотного колебания, т. е. что выполняется соотношение

(Оо tn - 2лп,

(5-49)

Это ограничение, ие являясь принципиальным, упрощает дальнейшие выкладки.

Спектр рассматриваемого сигнала в операторной форме может быть представлен в следующем виде:

S (со) =

2/сй

(О? -со

,-/( - 0) и( + )

,-/(° + 0) И( )

или с учетом (5-49) Р

S (со) = £

P + wg

(5-50)

Если реализовать фильтрующую цепь таким образом, чтобы выходной сигнал снимался с колебательного контура, настроенного иа частоту соо, равную частоте заполнения входного сигнала, и включенного

Рис. 5-87. Схема для оптимальной фильтрации прямоугольного радиоимпульса с отрезком неоднородной линии.

последовательно с отрезком неоднородной линии (рис. 5-87), то нужная для оптимальной фильтрации частотная характеристика фильтрующей цепи может быть он-, ределеиа путем замены в формуле (5-50) р иа -р и сдвига в области времени иа величину и. Последнее позволяет физически реализовать цепь, которая описывается выражением

К{р)=В

,-Ри

p + w

р+<

отрезок линии должен обладать входным сопротивлением вида

ex(p) = /?cth4-.

где А - некоторый постоянный коэффициент.

Можно показать, что для того чтобы амплитуда выходного сигнала была мак-

симальной, значение А следует выбирать из условия

Волновое сопротивление входящего в схему фильтра отрезка неоднородной линии должно изменяться при этом по закону

4 Г -- \ cos (Оо X йх

и J

sin too X dx

При значительных длительностях фильтруемого импульса схему фильтра удобно выполнять из сосредоточенных элементов, заменяя отрезок линии цепью параллельных контуров, соединенных последовательно (см. рис. 5-74). Параметры этих контуров должны быть рассчитаны по формулам (5-45). Выходной сигнал следует снимать с того контура, собственная резонансная ча-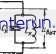

Рис. 5-88. Схема для оптимальной фильтрации прямоугольного радиоимпульса с эквивалентом отрезка неоднородной лнинн.

стота которого совпадает с несущей частотой радиоимпульса. Вместо /и в выражения (5-45) следует подставлять длительность радиоимпульса. На рис. 5-88 приведена схема фильтра в такой реализации.

5-12. ЛИНЕЙНЫЕ ЦЕПИ С ИЗМЕНЯЮЩИМИСЯ ПАРАМЕТРАМИ

Электрические системы, в которых хотя бы один из параметров (сопротивление, емкость, индуктивность) является переменным (зависящим от времени), называются цепями с переменными параметрами или параметрическими цепями.

Если параметры зависят только от времени и ие зависят от режима работы, система является линейной. Следует заметить, что в ряде случаев к рассмотрению линейных систем с периодически меняющимися параметрами сводится анализ нелинейных систем, находящихся под воздействием двух сигналов, один из которых значительно превышает другой.

С помощью параметрических систем, в которых переменным является активное со-

противление, могут осуществляться, например, такие преобразования сигналов: детектирование, выпрямление, амплитудная модуляция, различного рода преобразования частоты и т. д.

В цепях с переменными реактивными элементами, способными запасать и отдавать энергию, при определенных условиях могут происходить усиление и возбуждение колебаний. Это может быть связано с появлением в системе отрицательного сопротивления, описывающего формально физический процесс внесения колебательной энергии в систему за счет работы сил, периодически изменяющих параметр, и свидетельствует о наличии так называемой параметрической регенерации колебаний данной частоты. Под регенерацией, как известно, понимается процесс частичного восполнения теряемой в системе энергии.

Математическое описание процессов, происходящих в параметрических цепях, сводится к линейным уравнениям с переменными коэффициентами: в простейших случаях - к алгебраическим, а в более сложных - к дифференциальным. Теория этих уравнений относительно сложна и недостаточно разработана, поэтому общего метода решения подобных уравнений ие существует. Имеется лишь достаточно полная теория уравнения Хилла, имеющего вид:

x + [a+qf(t)\x.O, ,

где /(/) - периодическая функция времени. Частный вид уравнения Хилла

х -Ь (G-Ь 29 cos 20 л: = О (5-51)

называется уравнением Матье. Эти уравнения успешно применяются при анализе усиления и возбуждения колебаний за счет периодического изменения параметров

Параметрическое усиление и возбуждение колебаний

Рассмотрим колебательный контур, емкость которого является периодической функцией времени. Аналогичный анализ может быть проведен и для переменной во времени индуктивности (рис. 5-8Э).

Уравнение напряжений для этой схемы имеет вид:

1ц гЩЛ-

* =0, (5-52)

Рис. 5-89. Колебательный контур с переменной во времени ем-

костью.

где q - заряд иа емкости.

Пусть периодическое изменение емкости контура осуществляется по синусоидальному закону с помощью напряжения с частотой (Он и пусть зависимость емкости от напряжения имеет вид:

С = /( ) = во + 1с+ 2с+--- (5-53)

Такой случай может быть, например, если в качестве емкости контура используется зависящая от напряжения емкость р-п перехода полупроводникового диода, смещенного в обратном направлении. Подставляя в выражение (5-53) значения Uc = - Ucosant и заменяя степенной ряд соответствующим рядом Фурье, получаем:

С (f) = Со + Ci cos (Он + Са cos 2(Вв < Н----

Ограничиваясь двумя первыми членами, выразим емкость контура в виде

C{f) = Co(\ + т cos (Ои t), (5-54)

m=Ci/Co - коэффициент модуляции емкости. (5-55)

С учетом выражения (5-55) и в предположении, что /п С 1, соотношение (5-52) может быть переписано в виде

д + 2д,д+(4{l+mcos(uj)q==0, (5-56)

26 = -

С помощью

подстановки

уравнение (5-56) сводится к виду

у + {al + malcosvigt ) у = 0, (5-57)

не содержащему члена с первой производной. В этом уравнении cui= )/(b2 g2

собственная частота контура с параметрами L, /? и Со.

Если в уравнении (5-56) положить (йн=2т (т-безразмерное время) и заменить производную по t производной по т, получим:

(а\ 4 \

+ 4 -T+-r cos2T j, = 0. (5-58)

Сравнение уравнений (5-58) и (5-51) свидетельствует о том, что уравнение (5-58) является уравнением Матье. Общее решение такого уравнения складывается из двух независимых решений в виде

у = Ле Qi (т) + Фа (т); (5-59)

здесь Л и б - произвольные постоянные; ф, и Фа - периодические функции времени с периодом п или 2зт, а ц - показатель, определяемый коэффициентами ш/ю и (Oo/to уравнения (5-58).

Вопрос о самовозбуждении или об усилении в системе, описываемой уравнением (5-58), сводится к нахождению тех условий, при которых решения становятся неустойчивыми. Очевидно, что если р. является действительным и не равным нулю числом, то одно из слагаемых выражения (5-59) неограниченно возрастает с увеличением т, что свидетельствует о неустойчивости решения. Анализ показывает, что в слу-

чае неустойчивости выполняется неравенство

I I > - . (5-60)

Это неравенство является условием самовозбуждения рассматриваемого контура.

Результаты приближенного анализа неустойчивости решений уравнения (5-58) представлены на рис. 5-90. По оси абсцисс отложено отношение удвоенной частоты собственных колебании контура к частоте модуляции параметра. По оси ординат от-

Рвс. 5-90. Области неустойчивости системы с периодически изменяющейся реактивностью.

ложеиы значения коэффициента модуляции т. Заштрихованные области являются областями неустойчивости, соответствующими параметрическому возбуждению. Кривые, отделяющие заштрихованную часть от не-заштриховаииой, представляют собой геометрические места критических значений коэффициента Откр, при превышении которых система возбуждается. Из приведенных графиков следует, что колебания легче всего возбуждаются на частоте, равной половине частоты модуляции параметра: 1

(йо =

СОв.

(5-61)

При этом, как показывает расчет,

т > 2d, (5-62)

где d - затухание контура.

При значениях т<тк-в в системе будет наблюдаться усиление. Границы областей возбуждения призаданном затухании зависят от глубины модуляции параметра т. С ростом активного сопротивления контура области возбуждения сужаются. Частоты, .при которых возможно возбуждение, лежат около значений

= п, где п= 1,2,3

Заметим, что чем больше номер гармоники, иа которой возбуждаются колебания, тем большая глубина модуляции требуется для их возбуждений. Например, для второй области неустойчивости необходима модуляция /п > 2d, для третьей т>1,84

d и т. д.