Плотность тока смещения дЕ до

JCM = fa

dt dt

(4-95)

Таким образом, ток в цепи оказывается замкнутым: линии тока в проводах продолжены линиями тока смещения между обкладками.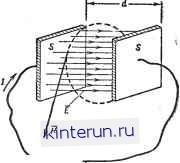

-0ц 0

Рис. 4-33. к определению тока смещения.

Для медленных электрических процессов (постоянным ток, низкие частоты) токи смещения себя ие проявляют. Но для быстропеременных электрических процессов полный ток в данной точке пространства нужно считать равным сумме тока проводимости н тока смещения:

1полн - j +

ар di

(4-96)

Уравнения Максвелла

Введение тока смещения как одного из источников магнитного поля позволяет сформулировать полную систему уравнений, устанавливающих связь электрических и магнитных полей между собой, а также с их источниками (зарядами и токами).

Интегральный вид уравнений Максвелла

Закон полного тока (см. §. 4-4):

ф Hds = J j dS-f j dS. (4-97)

С s s

Закон электромагнитной индукции (см. § 4-5):

Eds=-fBdS. С s

(4-98)

Теорема Гаусса, устанавливающая связь электрического поля с его источниками

(электрическими зарядами) (см. § 1-15 и 4-2):

DdS = JpdV.

(4-99)

Соотношение, устанавливающее отсутствие в природе магнитных зарядов (см. § 4-4):

BdS = 0.

(4-100)

Для того чтобы учесть основные электрические свойства среды, к этим уравнениям необходимо добавить линейные зависимости между векторами электромагнитного поля (см. §§ 4-2-4-4):

3 = 0Е; (4-101)

D = eaE; (4-102)

B=HaH.g (4-103)

Дифференциальный вид уравнений Максвелла

Воспользовавшись теоремой Стокса и теоремой Гаусса - Остроградского (см. § 1-15), можно представить уравнения электромагнитного поля в виде следующих дифференциальных соотношений:

1) rotH = j +

2) rot Е =

3) div D = р;

4) div В = 0.

(4-104)

(4-105)

(4-106) (4-107)

Линейные соотношения между векторами поля, учитывающие электрические свойства среды, остаются прежними.

Уравнения Максвелла (и его гипотеза о токе смещения) не являются результатом строгого математического вывода. Доказательством этих уравнений является волновой характер распространения электромагнитных процессов и многочисленные практические подтверждения выводов, вытекающих нз этих уравнений.

Волновые уравнения

Решение уравнений Максвелла в большинстве случаев сводится к решению волновых уравнений для векторов поля.

Волновые уравнения легко могут быть получены из первого и второго дифференциальных уравнений. Для этого сначала следует исключить векторы D = eaE и В = = НаН (считаем, что 8а и На не зависят ни от времени, ни от координат, т. е. среда однородна и изотропна). После этого ко второму уравнению применяется операция ротора и с помощью первого уравнения ис-

ключается вектор Н. Имея в виду, что для любого вектора А

го1 rot А = grad div А - уА,

легко получим волновые уравнения

+ - gradp;

VH-ваЦа-= rotJ.

(4-108)

(4-109)

Здесь для краткости символом обозначен оператор Лапласа (лапласиан). В прямоугольной системе координат для любого вектора

A:=iAj, + iAy + kAi

лапласиан

А = i + i vMj, + к vM,

и т. д.

Для решения волновых уравнений необ-.аддимо знать распределение (в пространстве и во времени) источников поля (токов j и зарядов р).

Но волновые уравнения имеют ненулевые решения и для тех областей пространства, в которых j=0 и р=0, т. е.

VE-eaiia = 0: (4-110)

(4-111)

Это означает, что при определенных условиях электромагнитное поле может потерять связь со своими источниками и существовать самостоятельно при полном отсутствии токов и зарядов. Подобные электромагнитные поля называются электро-м а г и ит ными волнами. Эти волны распространяются в пространстве с конечной скоростью (см. § 6-1).

Плоские электромагнитные волны в идеальном диэлектрике

В идеальном однородном диэлектрике свободные заряды отсутствуют (р==0), а электрические параметры не зависят от координат точки наблюдения, причем о=0. Для этого случая можно найти решение волнового уравнения, которое зависит лишь от координаты вдоль одного направления (например. Ох) и остается неизменным в каждой плоскости (yOz), перпендикулярной этому направлению. Электромагнитное поле, соответствующее этому решению, называется плоско й электромагнитной волной. Составляющие векторов

плоской волны могут быть представлены в виде

/ X \ Ez = f\t::ii~j; Ех==Еу = 0;

(4-112)

называется скоростью распространения волны (м/сек).

Знак минус в этом решении соответствует бегущей волне, распространяющейся в направлении оси Ох, а знак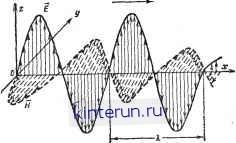

Рис. 4-34. Напряженности электрического и магнитного полей плоской воЗгны,

плюс - волне, распространяющейся в обратном направлении. Эти две волны распространяются независимо друг от друга, и результирующее поле представляет собой сумму этих волн. Однако если отражения волн не происходит, то обратная волна отсутствует и в формулах следует оставить лишь верхний знак.

Вид функции f

1 V 1

зависит от на-

чальных условий. Для радиоволн наибольшее значение имеют периодические функции, т. е. (рис. 4-34)

Ег = Ет cos ю

Ex=Ey=Q; (4-113)

fcoscu

(4-114)

я = я = о.

Чтобы получить наглядную картину распространения плоской волны, необходимо представить, что графики на рис. 4-34 перемещаются вдоль оси Ох со скоростью Р.

Плоская волна в идеальном однородном диэлектрике является поперечной волной (в ней отсутствуют составляющие поля вдоль оси распространения).

Электрическое и магнитное поля плоской волны распространяются с одной и тон

же скоростью и в каждой точке пространства имеют одинаковую фазу.

Поверхность, во всех точках которой фазы колебаний одинаковы, называется фронтом волны. В плоской волне фронтом волны является плоскость, перпендикулярная направлению распространения. Скорость V, с которой фронт волны перемещается в пространстве, называется фазовой скоростью. Она определяет скорость распространения лишь фазы, но не энергии электромагнитной волны.

В свободном пространстве фазовая скорость равна скорости света

с= x3-W м/сек, (4-П5) а в идеальном диэлектрике (е = const, [х = 1)

(4-116)

V =

Расстояние, проходимое фронтом волны за один период Tl/f колебаний, называется длиной волны

l = vT =

(4-117)

Длина волны является ее пространственным периодом (рис. 4-34), т. е. наименьшим расстоянием между точками, в которых колебания имеют одинаковую фазу (точнее, отличающуюся на 2я).

Фаза колебаний в бегущей волне линейно зависит от расстояния

ф = - х = ах,

(4-118) (4-119)

называется волновым числом (постоянной распространений).

Отношение амплитуд напряженностей электрического и магнитного полей в плоской волне носит название волнового сопротивления среды

Для свободного пространства

Zo = l/ - =120 я = 376,6 ол.

Перенос электромагнитной энергии волной характеризуется вектором Умо-ва - Пойнтинга

р = ЕХН, em/л (4-121)

который определяет плотность и направление потока энергии, т. е. количество энергии, проникающее в единицу времени через единичную площадку, нормальную к вектору р.

В плоской волне плотность потока энергии и действующие значения напряженностей связаны следующей зависимостью:

Й = £Я =

£2

= №Zo. (4-122)

Например, волна, распространяющаяся в свободном пространстве с плотностью потока энергии 1 мквт1м\ обладает действующим значением напряженности электрического поля

Е = Ур-ттс =К10-в.120я = = 19,4-10-3е/л ~ 20 мв1м.

Плоские электромагнитные волны в проводящей среде

В природе идеальные диэлектрики отсутствуют; любая среда обладает некоторой проводимостью. Вопрос о том, куда следует отнести данную среду - к ди-диэлектрику, полупроводнику или проводнику, решается по соотношению между током проводнмостн

] = оЕ

и током смещения

3см - 8а

Это соотношение зависит не только от параметров среды, но и от скорости изменения электрического поля во времени. Например, для гармонически изменяющихся полей

/сн ЕаСО

(4-123)

При -:-<<1 среда считается диэлект-/см

риком, при-7->>1-проводником, а при /см

7- 1 - полупроводником, /см

Для идеального, диэлектрика (а=0) первое дифференциальное уравнение Максвелла (см. ур-е 4-104) имеет вид

rotH=ea---, at

а для проводящей среды йЕ

rotH = ea-r-+ оЕ. at

Но для гармонически изменяющихся по-

Е = Е, е/

после дифференцирования получим:

(й dt