Аяалга.и сынтеа алектропривода непрерывного действия

начинается расчет и в каком порядке он ведется [9.7].

Точность расчетов методом конечных приращений зависит от вида функции и шага интегрирования Д<. Чем меньше Д/, тем выше точность, но это ведет к увеличению шагов интегрирования н повышению затрат времени на проведение расчетов. Практика расчетов показывает, что в системах электропривода дли получения приемлемой точности достаточно At выбрать в 3-i раза меньше минимальной вз учитываемых в расчете постоянных времени.

Если применять метод конечных приращений для расчета переходных процессов в разомкнутых системах электропривода, то точность его будет низкой вследствие накопления ошибки от шага к шагу. В замкнутых же системах электропрнвода ошибка компенсируется действием отрицательных обратных связей, которые стараются восстановить требуемое значение переменной, т. е. если ошибка возрастает, обратная связь на следующем шаге уменьшает значение переменной. Это приводат к разбросу расчетных точек, через которые проводится средняя линия, достаточно точно характеризующая переходный процесс.

Метод фазовой плоскости (каноняческнх полигонов) получил распространение для анализа переходных процессов в нелинейных системах электропривода, описываемых дифференциальными уравнениями второго порядка [9.8]. Переходный процесс рассматривается на фазовой плоскости у = dx/dt ~ f (дс), иа которой каждому состоинию системы во времени соответствует одна точка, называемая фазой. Начальному состоянию соответствует начальнаи фаза, конечному (при установившемся процессе) - конечная фаза, называемая точкой покоя. При движении эта фаза вычерчввает на фазовой плоскости фазовую траекторию.

Задачей метода канонических полигонов ивляется нахождение фазовой траектории, соответствующей требуемому переходному процессу, и нахождение по фазовой траектории самого переходного процесса во времени.

При этом решаются два дифференциальных уравнения первого порядка, записанные относительно производных:

=Р(*.)5

-Q(x, у).

где Р (х, у) и Q (х, у) - любые линейные и нелинейные функции отхиу, задаваемые аналитически илн графически.

Функции Р (х, у) л Q {х, у) образуют на фазовой плоскости векторное поле так называемых мгновенных фазовых скоростей

Р{х. y)l+Q(x, у)7,

где 7*и 7*- единичные векторы скорости, направленные в горизонтальном и вертикальном направлениях на фазоврй плоскости.

Скорость и направление (рис. 9.16, а) движения фазы определяются вектором поля, тангенс угла наклона сс которого относительно оси абсцисс определяется как

dy Idx dy Q{x. у)

и-------

tg06 =

dt dx P(x.y)

Направление вектора поля определяется знаками производных dy/dt и dx/dt.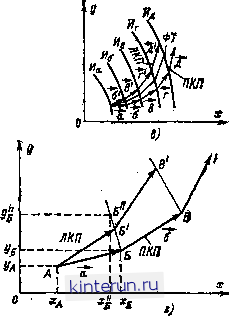

Рве. 9.16. Заввовиоств, аллюстрнрующве иетод фазовой плоскости: ваправлеиия вектора поля (а), вулевая и бесковечваи изоклины (б); построение право- в левокавоивческвх полвровов ПКП, ЛКП я фазовой траектории (Ф7) ( ); па-строение участка вэоклявы БВ (а).

При построении фазовой траектории необходимо строить изоклины или часть их. Изоклина - это геометрическое место точек на фазовой плоскости, где tga = const При tg а = О изоклина называется нулевой, на которой Q X {х,у)= Он вектор поля определяется только горизонтальными Лекторами Р (х, у). При tg а = оо изоклина бесконечная. На ней Р {х, у) = О я вектор поля определяется только вертикальными векторами Q (X, у) (рис. 9.16, б). При tga = А изоклина называется -й.

Анализ и синтез автоматизированного электропривода

{Раэд. 9

Фазовая траектория находится с помощью правокаяоиического и левокаиоиического полигонов, построенных из так называемых отрезков односторонней проводимости (рис. 9.16, в). Правоканоннческий полигон ПКП строится по направлению векторов поля, принадлежащих своим изоклинам Иа, Иб, Ив, Иг (векторы, Ъ,Т,Т, д), г левокано-нический полигон ЛКП строится по направлению векторов поля, принадлежащих соседним расчетным изоклинам Иб, Ив, Иг, Иб (векторы3,в,г, Э), проведенные параллельно векторам б, 7, 3 соответственно. Фазовая траектория ФТ проводится посредане между полигонами.

Порядок построения фазовой траектории может быть принят следующий. Сначала строятся нулевая (НИ) и бесконечная (БИ) изоклины (рис. 9.16, б) по уравнениям Q (х, у) = Q п Р (х, у)= О соответственно, и находится точка покоя ТП на пересечении этих изоклин, где Q (х, у) - О и Р (х, у) = 0. Затем строятся правый ПКП и левый ЛКП канонические полигоны (рис. 9.16, г). Построение начинается с начальной фазы А, определяемой начальными условиями (х = Xj, у = - yj, в которой находится тангенс угла наклона вектора поля

Из начальной фазы проводится вектор поля а. Построение вектора поля производится исходя из того, что на участке между соседними расчетными изоклинами вектор не меняет своего направления и

Это облегчает расчет и учитывает любые масштабы по осям хлу. Далее в направлении вектора а делаетси произвольный шаг до точки Б (тем меньший, чем выше желаемая точность построения). В точке Б по ее координатам Xg и у снова определяется тангенс

угла наклона вектора поля б

* е = Д?-р(Хз, уу

Для построения правоканонического полигона иектор В проводится из точки Б до точки В, определиемой следующим произвольным шагом. Для построения левоканоннче-ского полигона вектор б* проводится из точки А до Б, принадлежащей изоклине, которая проходит через точку б. Для нахождения точки Б строится участок этой изоклины. Считая участок изоклины между точками Б л Б прямолинейным, находят произвольную точку Б, принадлежащую этой же изоклине, исходя из того, что

. У Б) ,

Подставляя сюда значение Xg (или у ), несколько отличающееся от х (или у), находят значение у (или Xg ). Пря этом точка Б является точкой пересечения вектора б и участка изоклины Б-Б или его продолжения, если точка Б находится между точками Б л Б. Практически в системах электропривода, у которых коэффициещт передачи системы гюстояиен или близок к постоянному значению, изоклины предстаиляют собой прямые линии (или близкие к прямым), проходящие через искомую точку и точку покоя. Поэтому участок изоклины Б-Б° не рассчитывается, а принимается в виде отрезка прямой, проходящей через точку Б и точку покоя. , .

Дальнейшее построение полигонов прЪ-изводится аналогично до тех пор, пока фазовая траектория, проводимая и середине между полигонами, не придет в точку покоя. Расчетные значения правоканонического поли; гона обычно заносятся в расчетную таблипцг.

Переходный процесс во времени находится по фазовой траектории с помощью графического интегрирования одного из уравнений Р (X, у) или Q (х, у).

При анализе переходных процессов и системе электропривода с безыиерциоииым преобразователем, прииедениой иа рис. ffjl, расчетные уравнения записываются слеяу)р щим образом:

13+ ЕИо,с = Иу:

di в -©/Ад-17?

- = Р( , 0;

da dt

-7jr

=Q(®, О-

Тангенс угла наклона вектора поля

tga =

Q(<o. i)

p(©, 0 (в -в/Лд- )/в:

Время переходного процесса при Графическом интегрировании уравнения Q (<й:.()

Д<,

т+1 = пг + Д

Метод канонических полигонов проД и наглядный. Он позволяет получить решения при любом количестве и виде нелинейностей. Точность расчетов может быть высокой, так как коридор между полигонами можно ие-ограничеино сужать. Характерной особенностью метода является возможность оценки характера переходного процесса и устойчивости нелинейной системы электропривода по фазовой траектории без расчета переходного процесса. Недостатком метода является возможность его использования для анализа прог пессов в системах не выше второго порядка..

Метод математического мохелкромяия представляет собой экспериментальное исследование переходных процессов системы авто-

матйзироваииого электропривода на ЭВМ как аналоговых (АВМ), так и цифровых. Метод основан иа идентичности дифференциальных уравнений исследуемой системы электропривода и математической модели (аналога), исследуемой на ЭВМ [9.10, 9.11]. Физическая сущность оригинала и модели может быть различна. АВМ позволяет анализировать пёреходаые процессы, имеющие место в системах автоматизированного электропривода с линейнымя и нелинейными характеристиками. Эффективность исследования процесса АВМ, позволяющая производить инвариантные расчеты с разными коэффициентами и параметрами, дает возможность использовать машину для синтезирования систем электропривода, т. е. для проверки правильности вйбора как параметров исследуемых систем, так и целых звеньев, обеспечиваюпшх требуемое качество переходных процессов. Основное время при математическом моделировании иа АВМ затрачивается на составление Д!Пференциальиых уравнений, подсчет коэффициентов и набор модели на машине. Составление дифференциальных уравнений, описывающих переходные процессы в исследуемой системе автоматизированного электропри-йода, может производиться любыми методами. Однако наибольшее распространение полу-<тл структурный метод, когда набор задачи нИ -машине производитси по структурной схеме исследуемой системы, где каждое звеио характеризуется своей передаточиой функцией или дифференциальным уравиеиием первого или второго порядка. Это позволяет осуществлять набор задачи небольшим числом элементов модели, соответствующих типовым звеньим системы электропривода, создает ясное представление о соответствии величины и параметров в исследуемой системе и модели, что удобно при подборе корректирующих звеньев.

Переходные процессы в простых типовых звеньях исследуемой системы воспроизиодятся иа АЁМ с помощью операционных усилителей (усилителей постояииого тока с иысокими коэффициентами усиления ky > 10*, работающих с сильной отрицательной обратной связью). Вследствие свойства ииверсиости операционных усилителей нечетное число каскадов усиления, обычно равное трем, позволяет менять знак на выходе усилителя и рщает введение отрицательной обратной

Передаточная функция такого усилителя Ш. 9.17)

ip)-

Цвых(Р) Ивх(Р) о.с(Р)

ZbAp) + Zo,c(p)

kit,)

где Zo,c (Р) изображение сопротивления обратной связи; Zbx (р) - изображение со-протнвлеиня, включаемого на входе усилителя; ky - коэффициент усиления усилителя по напряжению в разомкнутом состоянии.

Так как при высоких зиачеииях ky nip).

то передаточной функцией операционного усилителя считается

W(P) =

BMl(P) Zo,c(P)

ZniP)

(9.32)

В зависимости от вида сопротивления элементов, включаемых на входе и в обратную связь усилителя, входная и выходная переменные связаны соответствующими, математическими зависимостями (табл. 9.3).

Ч& о-

Рнс. 9.17. Схема включения операциовиого уев-лителя.

При включении иа вход и и обратную связь усилителя активных сопротивлений (2, >= = Zo,e = Re) его выходаое иапряжеине согласно (9.32) оказываетси равным

Ивых=- вх.

Следовательно, усилитель осуществляет умножение входаого сигнала на постоянный коэффициент с одновременным изменением знака. При Ri = Ri = R усилитель осуществляет инвертирование, т. е. только изменение знака.

При включении на вход усилители емкости (р) = 1/Свхр, а в цепь обратной связи активного сопротивления Zip) = R передаточная функция усилителя соответствует дифференцирующему звеиу

W(p) = --/?o.cC,xp. Выходное напряхсение усилителя пря

этом

**вх

Ивых Ro, сРвх

Т. е. усилитель дифференцирует входной сигнал с постоянной времени 7= Ro,cCbz-

Если иа вход усилителя включить акгвв-ное сопротивление Zj (р) = R , а и обратную связь - емкостное Zo,e {р) = 1/Со,сР то передаточнаи функция соответствует интегрирующему звеиу:

W{p)--1/RbxCo,cP.

Выходное напряжение усилителя

вых--

Raxo

Jubx*.

и усилитель интегрирует входной сигнал с постоянной времени Т = RbxCo,c-