и фазовый портрет системы для каждого значения а представляет собой эту линию тт.

Исходное (начальное) состояние системы задается точкой А на фазовой траектории. При изменении параметра а меняется фазовая траекторая. Совокупности значений а соответствует семейство (совокупность) фазовых траекторий (рис. 21-96,6), которую также можно назвать фазовым портретом системы. Изображающая точка, характеризующая состояние системы, может двигаться вдоль кривой на рис. 21-96,0 или вдоль любой из кривых, изображенных на рис. 21-96,6, но, конечно, не может переходить с одной кривой на другую.

Рассмотрим движение рабочей точки, начиная с исходного состояния, например А0 (рис. 21-96,0). Так как скорость у=х этой точки положительна, х возрастает и точка движется вправо со все увеличивающейся скоростью. После прохождения максимума кривой (точка Ат) скорость движения изображающей точки замедляется и в Л4 точка останавливается (скорость ф=0). Это состояние системы будет равновесным. Состояние At устойчиво, поскольку при отклонении от этой точки вправо или влево скорость становится соответственно отрицательной или положительной и система возвращается в состояние равновесия At. Напротив, состояния равновесия Аи А2 и А3 (где у также равно нулю) будут неустойчивыми, поскольку малейшее отклонение от них уводит изображающую точку от этих состояний. Рассмотрим движение системы в случае, когда начальное состояние системы задается точкой Aq. Изображающая точка перемещается вправо (так как *>0), пока не достигает точки М, где производная функция ф терпит разрыв (бесконечна): dtyldx- со. Это означает, что не существует однозначного решения уравнения (21-141) и заранее нельзя сказать, как будет вести себя система при достижении этой точки, если не ввести в рассмотрение дополнительные факторы, характеризующие данную систему.

При составлении уравнения (21-141) обычно делаются некоторые упрощения, например не учитывается действие инерцион-ностей с малыми постоянными времени. Это справедливо, пока система не достигла состояния М. Теперь, чтобы установить характер движения в системе, нужно привлечь дополнительные данные. Одним из них является положение о том, что в системе возможны только такие скачки скорости (при неизменной координате), которые не приводят к скачкообразному изменению энергии, так как при скачках энергии требуется источник бесконечной мощности.

Учитывая указанное дополнительное положение, приходим к заключению, что система, достигнув точки М, скачком перейдет на нижнюю ветвь кривой в точку Р и будет двигаться затем влево (в сторону уменьшения х, поскольку у<0) до тех пор,

пока не придет в состояние N. Здесь система скачком перейдет в состояние Q. В результате в системе возникнут периодические движения (автоколебания). Они возможны вследствие того, что функция ф(х) имела обращающиеся в бесконечность производные; если бы функция ф была аналитической, периодические процессы в системе были бы невозможны.

Автоколебания в рассматриваемой системе возникнут только в том случае, когда начальное состояние системы лежит между точками Ах и As. В противном случае система придет к одному из устойчивых состояний равновесия, например, At и будет оставаться там сколь угодно долго.

Из приведенного примера видно, насколько разнообразны движения в нелинейной системе и как наглядно с помощью метода фазовой плоскости выявляется характер всех возможных движений.

Если имеется необходимость определить время установления процессов, необходимо вычислить интеграл (21-142) при заданных начальных условиях; фазовый портрет дает четкое представление о том, какие движения происходят при этом в системе.

Указанный метод использован в дальнейшем для анализа нелинейных режимов в системе слежения за частотой (см. стр. 171).

Системы второго порядка. Автономная система второго порядка списывается одним уравнением второго порядка вида

у=1р{х,у). (21-143)

Обозначая х=у, вместо одного уравнения (21-143) получим систему двух уравнений первого порядка:

y = Hf(x,y); \ х = У, I

которую обычно - записывают в более общем виде:

(21-144)

У = Р(х, у); 1 * = <2 (х,у), )

(21-145)

где Р и Q - некоторые функции переменных х и у.

Состояние системы в любой момент времени характеризуется точкой (координатой х и скоростью у=х) фазовой плоскости. С течением времени состояние системы меняется и изображающая точка х, у перемещается по некоторой кривой, которая называется фазовой траекторией. Совокупность фазовых траекторий, соответствующих всем возможным начальным состояниям системы, образует фазовый портрет, который позволяет рассмотреть совокупность всех возможных движений в системе.

Исключим из уравнений (21-144) и (21-145) время, поделив одно на другое:

dy ф (х, у)

или в более общем виде

dy dx

Р (х, У)

Q(x,y)

(21-147)

Решением этих уравнений является семейство кривых у-{(х, С) на плоскости, зависящее от постоянной С. Каждому значению С соответствуют определенные начальные условия. Кривые y=f(x, С) на плоскости х, у называются интегральными. С помощью равенств (21-146) и (21-147) определяются направления касательной в любой точке интегральной кривой, где выполнены условия существования однозначного решения Коши (см. т. 1, стр. 33). Интегральные кривые ие всегда идентичны фазовым траекториям. Возможны случаи, когда одной интегральной кривой соответствует несколько фазовых траекторий. В нашем случае неоднозначность появляется в точках (х0,. Уо), где одновременно выполняются условия:

для систем, описываемых уравнением (21-146),

Ф(*о, Уо) = О

(21-148)

или функции Р и Q не определены;

для систем, описываемых уравнением (21-147),

( Р{х0, у о) = 0; I Q(*o, Уо) = 0

или в точках, где функция ф не определена.

В дальнейшем ограничимся рассмотрением системы, описываемой уравнением (21-146). Система будет находиться в состоянии равновесия, когда скорость и ускорение равны нулю, т. е.

dx dt

d2x dy

- О; -- =

dt2 dt

= 0.

Из уравнения (21-144) видно, что dx\dt=y, dy/dt=ty. Следовательно, состояниям равновесия отвечают точки, в которых выполняются равенства:

у = 0; ф (х, у) = 0.

Но именно такие точки согласно равенству (21-148) будут особыми. Следовательно, точки, в которых система находится в состоянии равновесия, являются особыми, т. е. состояния равновесия одновременно являются такими точками фазовой плоскости, где касательные к интегральным кривым являются неопределенными.

Для выявления состояний равновесия и определения, являются ли эти состояния устойчивыми, необходимо построить фазовый портрет вблизи особых точек.

Если перед исследованием поставлена задача рассмотреть характер движения вблизи состояний равновесия, систему следует линеаризовать и построить фазовый портрет этой линеаризованной системы. На рис. 21-97 изображены различные типы осо-9-1248

бых точек линеаризованной системы второго порядка (стрелками указано направление движения изображающих точек). Здесь также изображены временные характеристики процесса вблизи особых точек (исходные состояния на фазовых траекториях обозначены точками Лв), причем каждому начальному значению координат хв и уп точки Ак соответствует своя интегральная кривая. Интегральные кривые могут пересекаться только в особых точках.

{.Центр - фазовые траектории являются эллипсами, охватывающими особую точку О. Корни уравнения первого приближения являются мнимыми. В этом случае нельзя ответить на вопрос, является лн состояние равновесия О исходной нелинейной системы устойчивым по Ляпунову.

2. Фокус - соответствует комплексным корням характеристического уравнения и соответствует устойчивому состоянию (вещественные части - отрицательные) или неустойчивому состоянию (вещественные части - положительные) равновесия нелинейной системы (рис. 21-97,6, в).

3. Узел - соответствует двум вещественным корням и характеризует устойчивое (корни отрицательны) или неустойчивое (корни положительны) состояние нелинейной системы в точке О.

4. Седло - соответствует вещественным корням различных знаков и характеризует неустойчивое состояние равновесия исходной нелинейной системы.

Чаще всего интересуются поведением системы на всей фазовой плоскости, когда необходимо построить фазовый портрет. Для этого необходимо произвести интегрирование уравнения (21-146), решение которого дает семейство интегральных кривых.

Чтобы выявить характер интегральных кривых и вид фазового портрета без интегрирования уравнений, прибегают к построению изоклин. Изоклиной называется кривая, для которой угол пересечения с касательной является величиной постоянной. Для построения изоклин в уравнении (21-146) полагают величину dy/dx=l постоянной и для каждого значения I строят изоклину

, Ф (х, у)

где i - тангенс угла наклона касательных к интегральным кривым. При достаточно большом числе изоклин по стрелкам, указывающим направление касательных, выявляется качественно ход интегральных кривых на веер фазовой плоскости.

На рис. 21-97,6 нанесены несколько изоклин, которые в случае узла представляют собой прямые, выходящие из состояния равновесия. Стрелками указано направление интегральной кривой в точке пересечения с изоклиной.

Если имеется возможность нелинейную характеристику представить в виде отдельных отрезков прямых (полигональная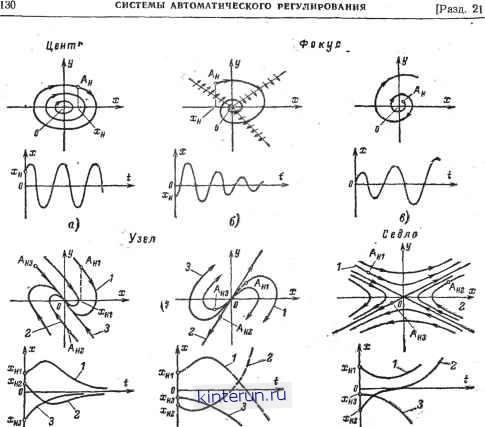

в) В) )

Рис. 21-97. Типы особых точек и характер переходных процессов вблизи них.

а - центр: б - устойчивый фокус; в - неустойчивый фокус; г - устойчивый узел; д - неустойчивый узел; е - седло: Аа- начальные изображающие точки; зсн - начальные величины.

аппроксимация), то нелинейное уравнение интегрируется для каждого такого отрезка в отдельности, а полученные отдельные решения сопрягаются (припасовываются) в точках излома характеристики. Фазовый портрет системы облегчает в этом случае выполнение операции припа-совывания и дает наглядное представление о свойствах системы.

Пример. Рассмотрим релейную следящую систему, в которой угол поворота выходного вала редуктора (0ВЫх) должен повторять угол 0ВХ перемещения движка входного потенциометра (рис. 21-98, а). При возникновении рассогласования между бвх и 0вых срабатывает поляризованное реле, через контакты / или 2 которого поступает напряжение U? на управляющую обмотку реверсивного исполнительного двигателя и якорь последнего поворачивается, перемещая движок в сторону уменьшения напряжения на реле. Структурная схема (рис. 21-98, б) системы состоит из релейного элемента и линейной части с передаточной функцией

где величина А учитывает коэффициент передачи всех элементов системы кроме реле (от выхода реле и до угла 0ВЫх).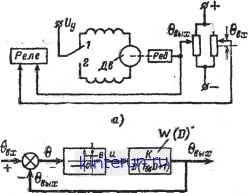

Рис. 21-98. Нелинейная система автоматического

регулирования. а - функциональная схема; б - структурная схема.