следовательно (рис. 21-4&75), Кэ

т2р2+2£тр+1

Кэ =

к + \

2\<ГТ1Т2(К+1)

Так как знаменатель передаточной функции W(p) не содержит множителей р (нет интегрирующих звеньев), система АПЧ является статической.

Замкнутая система АПЧ с однбзвен-ным фильтром эквивалентна инерционному звену с коэффициентом передачи KIK+1 и постоянной времени тэ, в К+\ раз меньшей постоянной времени Г-фильтра. Система с двухзвенным фильтром эквивалентна звену второго порядка.

Отсюда следует, что процессы в системах АПЧ совпадают с процессами в инерционном звене и звене второго порядка н для описания свойств таких систем следует пользоваться характеристиками инерционного звена и звена второго порядка (стр. 19 и 22).

Пример 2. Рассматривается автоматический радиопеленгатор (рис. 21-5). Напряжение на выходе фазового детектора (ФД) радиопеленгатора (см. стр.. 10) для небольших рассогласований пропорционально углу отклонения радиостанции от оси 00:

Участок схемы от точки подачи рассогласования до выхода ФД представляется пропорциональным звеном К\. Коэффициент Ki (размерность - в в/град) зависит в основном от крутизны диаграммы направленности в рабочей точке О, а также от усиления ФД. Далее следует усилитель с коэффициентом К2 н двигатель с переда-

Крв .

точной функцией ------ (см. стр. 26),

Р (7двР + 1) причем Ддв - коэффициент передачи двига-. теля с учетом редуктора (размерность - в град/в сек). Учитывая, что 0=0Вх- -©вых, получаем следящую систему, структурная схема которой состоит из трех звеньев (рис.. 21-49, а): усилительного с коэффициентом передачи Kv=KiK2KKb (размерность- б 1/се/с), интегрирующего (1/р)

С * \

и инерционного ~-- I .

\Тдв Р+ 1/ Замкнутая система описывается передаточной функцией

Ф(Р)-

p(T№p+\) + Kv

: т2р2 + 2 £тр + 1

= 4

V к

Система эквивалентна динамическому звену второго порядка, свойства которого рассмотрены на стр. 22.

При учете инерционных свойств фазового детектора в структурную схему (рис. 21-49, а) добавляется .инерционное звено с постоянной времени Т, вследствие чего степень полиномов знаменателя W и Ф увеличивается на единицу:

W(p) =

р(ГДБр+1)(Гр + 1) Ф(р) =

Kv

Р(7двР+1КТр+ D + Kv

(21-23)

(21-24)

(21-22)

Рассматриваемая система является астатической поскольку содержит одно интегрирующее звено [множитель р в знаменателе W(p)].

21-5. УСТОЙЧИВОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

Необходимым условием работоспособности системы автоматического регулирования является ее устойчивость.

Наиболее удобным и широко используемым является определение устойчивости, сформулированное А. А. Ляпуновым (см. §21-12).

Для того чтобы установить, устойчиво ли состояние равновесия, необходимо к системе приложить некоторое возмущение (отклонить систему от состояния равновесия) и рассмотреть движение системы после снятия возмущения (т. е. собственное движение системы). Для линейных систем достаточно следующее определение устойчивости. ч

Устойчивой называется линейная система, которая цосле прекращения действия возмущающих сил стремится к исходному состоянию, т. е. начальные отклонения стремятся к нулю.

Неустойчивая линейная система удаляется от состояния равновесия так, что отклонение от этого состояния непрерывно нарастает со временем.

В тех случаях, когда движение линейной системы не стремится к нулю и не затухает, считается, что система находится на границе устойчивости. Прн малых изменениях параметров система переходит в устойчивую или неустойчивую; поэтому практического интереса такой режим не представляет.

Реальная неустойчивая система, удаляясь от состояния равновесия, при доста-

точно больших отклонениях переходит в нелинейный режим. Чаще всего в этих случаях возникают автоколебания (периодические колебания устойчивой амплитуды).

Для нелинейных систем необходимо оговорить степень начальных отклонений, поскольку система, может иметь несколько состояний равновесия, из которых одни являются устойчивыми, а другие - неустойчивыми (см. стр. 127).

Здесь рассматриваются только линейные системы.

Прямой путь определения устойчивости системы состоит в составлении уравнения, описывающего собственные движения системы и исследовании решения этого уравнения.

Дифференциальное уравнение составляется на основе передаточной функции 1 замкнутой системы:

M(D) М (р)

Ф (D) = -~- или Ф(р)=--,

У R (D) КН) R (р)

где М и R - полиномы относительно D или р:

M(D) = bBD + cZ) 1-1 + ... + bm;

R{D) = a0Dn + d/) -1 + ... + c

(причем для реальных систем т <п).

Дифференциальное уравнение, описывающее свободные колебания в системе, имеет вид:

Я(£>)©вых(Г) = О

ао/>0вых + ai£> -J0Bbi* -f

+ ... + ar

(21-25)

Соответствующее ему характеристическое уравнение (см. т. 1, стр. 42) получается из (21-25) заменой оператора D параметром Я:

аокп + аД -* + ... + а 1Я +

+ап = 0. (21-26)

Если все вещественные части корней этого уравнения будут отрицательными, движение системы будет затухающим и система устойчивой.

Если хотя бы один корень имеет положительную вещественную часть, система будет неустойчивой.

На практике для определения устойчивости линейной системы пользуются критериями устойчивости, т. е. правилами, с помощью которых можно определить, устойчива ли система, не прибегая к решению дифференциальных уравнений.

Критерии устойчивости

Существует несколько критериев устойчивости: алгебраический (Рауса - Гурви-ца), Михайлова, частотный (Найквиста - Михайлова), и др. Ниже рассматриваются критерии, наиболее часто применяемые в практике

Алгебраический критерий (Рауса - Гурвица). Для определения устойчивости по этому критерию составляется передаточная функция замкнутой системы

Ф(1)) = M(D)/R(D)

Ф(Р) =

М(р) R(P)

и рассматривается полином, ее знаменателя.

Система автоматического регулирования будет устойчивой, если все коэффициенты а , d, ап полинома

R(D) = a0D + а,/) -1 +

+ ... + a iZ> + ап (21-27)

R (р) = аор + а,р -1 + + ... + a ip + ап

положительны (необходимое условие) и, кроме того, выполняются следующие неравенства:

для системы третьего порядка (и=3);

aia2 - а0а3 > 0; для системы четвертого порядка (п=4):

аз [aia2 - ао °з) -?? а4 > °> для системы пятого порядка (fi=5): (ajC2 - аойз) (Озй4 - ОгОэ) - - (0404 - а0а5)2 > 0.

и т. д.

Невыполнение указанных неравенств свидетельствует о неустойчивости системы.

При выполнении необходимого условия (коэффициенты положительны и отличны от нуля) системы, описываемые уравнениями первого и второго порядков, являются устойчивыми, т. е. для таких систем необходимое условие является одновременно и достаточным.

В случае систем высоких порядков алгебраическим критерием пользоваться неудобно из-за громоздкости получаемых выражений.

Пример 1. - Автоматический пеленгатор при наличии фильтра с постоянной времени Т [стр. 47, формулы (21-23), (21-24)].

Передаточные функции разомкнутой и замкнутой систем будут соответственно:

W(p) = -:-- ;

ТТ№р* + (Т+Т)р*+р

Ф(Р) =

в Kv

TTABp3+{TRB + T) р2+р + /С0

следовательно,

R(p) = ТдвТр* + (Г в + Г)Р2 +

Здесь

Т**Т.

+ р + Kv Os = Ki>.

Необходимые условия устойчивости выполняются. Для системы третьего порядка, кроме того, должны выполняться неравенства:

Й1Й2 - а0а3 > О,

т. е. 1 дв + 7 - ГГдвД- >0

/с0<

ДВ

Обозначим

Ккр=,

! ДВ

(21-28)

Если KV>K P, т.е. если Л не удовлетворяет неравенству (21-28), система становится неустойчивой. В данном случае будут наблюдаться нарастающие колебания. В дальнейшем нарастание амплитуды колебаний приостановится или система выйдет из режима слежения, поскольку начнет влиять нелинейность характеристик усилн- тельных элементов

Коэффициент усиления, при котором система переходит от устойчивого состояния к неустойчивому, называют Критическим Кир.

Частотный (амплитудно-фазовый) критерий (Най-квиста - Михайлова). Критерий позволяет сделать заключение об устойчивости замкнутой системы регулирования по амплитудно-фазовым или логарифмическим характеристикам разомкнутой системы.

Вначале приведем определения для систем, устойчивых или нейтральных, в разомкнутом состоянии (ха-

рактеристическое уравнение разомкнутой системы не- содержит корней с положи-. тельной вещественной

частью)

Если точка с координа-тамн (-1, /0) не охватывается контуром,образован-=*ет ным амплитудно-фазовой \ характеристикой и положительной вещественной полу-осью, замкнутая система устойчива (рис. 21-50, а);

если точка (-1, /0) расположена внутри него, система неустойчива (рис. Рнс 21-50, б).

Если точка (-1, /0) лежит на амплитудно-фазовой характеристике, замкнутая система находится на границе устойчивости. При этом малейшее увеличение коэффициента усиления системы приводит к тому, что эта точка будет охватываться контуром и система станет неустойчивой.

На рис. 21-50, а, б приведены амплитудно-фазовые характеристики статической системы (устойчивой в разомкнутом состоянии) с передаточной функцией вида

W{P)~ (TlP+l)(T2p+l)(T3p+l)

Если передаточная функция системы является инерционным звеном или звеном второго порядка, то ее амплитудно-фазовая характеристика ни при каком К>0 не охватывает точки -1, /0, поэтому при любых К>0 такая система устойчива.

В случае, когда система содержит интегрирующие звенья, амплитудно-фазовая характеристика прн со-* 0 уходит в бесконечность, поскольку характеристическое уравнение имеет нулевые корни. Такая система будет нейтральной в разомкнутом состоянии. Для определения, будет ли она устойчивой в замкнутом состоянии, необходимо образовать замкнутый контур, дополнив .характеристику дугой окружности весьма большого радиуса от действительной положительной полуоси до бесконечно удаленной ветви характеристики по часовой стрелке, и воспользоваться сформулированным выше правилом. Амплитудно-фазовые характеристики системы на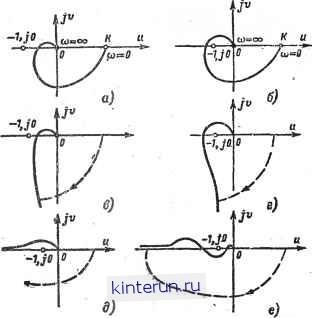

21 50 Использование амплитудно-фазовых характеристик для определения устойчивости следящих систем.