По окончании нескольких этапов поиска оператор оценивает результаты и выбирает наилучший. Выполнение описанного алгоритма предполагает интуитивно-эвристическое использование аналоговой схемы оператором, который, имея определенный набор сведений о существе исследуемой задачи, может уменьшать число бесполезных проб.

При поиске значений переменных, удовлетворяющих условиям (5.61) и (5.62), оператор может встретиться с положением, когда начальное положение изображающей точки оказывается вне области, и оператор яе сможет правильно выбрать переменные, изменение которых может привести к попаданию в область или уходу от границы. Чтобы облегчить работу оператора в этой ситуации, для образования функционала можно использовать более сложную зависимость

г =f(xi.....* ) + S Л:-

где ьесовые коэффициенты

а - = О при <ipy< 0; а. > 1 при <ff>0.

Метод Пайна.,Поиск решения задачи математического программирования может быть автоматизирован с помощью построения, предложенного Пайном для линейной задачи.

Образуем градиент функции г, который представляет собой постоянный п

вектор grad 2 = 2 tf где t,- - направляющие орты соответствующих ко-

ординатных осей, если рассматривать г как функцию в п-мерном пространстве. Вектор grad г определяет направление наибольшего возрастания функ цин г.

Образуем вектор = - 2 цЧ который перпендикулярен грани, огра-1=1

ничнвающей область возможных решений задачи, и направлен внутрь этой области. Рассмотрим точку внутри даииой области, определенную радиус-га

вектором -R = 2 подчиним движение этой точки определяющему урав-

нению

dt

k grad z+bjNi

= -if. (5.65)

где k и f - постоянные; 8 - функции вида

О, если 2 ifXibi,

=> (5.66)

1. если 2 1,Х1>Ь{.

1=1

Смысл уравнения (5.65) с условиями (5.66) состоит в следующем. Изображающая точка, начальное положение которой выбрано внутри обласси возможных значений Xi, движется в направлении наибольшого возрастания илн

убывания функции г (в зависимости от знака к) до тех пор, пока ие достигнет одной из граней гиперобъема, ограничивающего данную область. При этом согласно (5.66) соответствующая функция 6/ принимает значение 6у= 1; в результате этого направление вектора изменяется так, что изображающая точка вновь возвращается внутрь области возможных решений. Это движение для плоского случая изображено схематически иа рис. 5.18, из которого видно, что после достижания границы точка движется практически вдоль границы.

Искомому экспериментальному значению функции г соответствуют установившиеся значения переменных Х{.

С целью моделирования векторное уравнение (5.65) представляется в виде системы скалярных дифференциальных уравнений. Начальные значения переменных можно выбрать произвольно как в области возможных решений, так и вне области. При движении точки вне области движение происходит аналогично описанному, но точка сначала подходит к границе извне.

Значение постоянной k в уравнении выбирается с расчетом предотвратить прорыв изображающей точки за границу области. Для этого необходимо, чтобы выполнялось условие (-k grad zNj) < Nj для всех /. Постоянный коэффициент у имеет значение масштабного множителя, определяющего скорость протекания переходного процесса. Анализ знака ограничивающих соотношений (5.66) реализуется на АВМ с помощью переключательных элементов, моделирующих характеристику релейной функции.

Схема состоит из однотипных цепочек, образующих сигналы 6-, и суммирующих интегрирующих усилителей, вырабатывающих координаты фазоь вой точки. Для линейного программирования системы с п переменными и т ограничивающими условиями необходимо п интегрирующих усилителей, т усилителей анализа (5.66) и (п -f m) усилителей перемены знака. Общее число усилителей составляет 2 (п + т).

Таким образом, решение системы линейных неравенств сводится к решению системы определяюи1их дифференциальных уравнений (5.65). Метод определяющих уравнений можно применять также к решению на АВМ некоторых задач нелинейного программирования. Так, в частном случае нелинейной целевой функции г и линейных ограничений градиент г будет функцией координат:

9f -.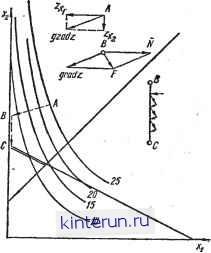

Рис. 5.18. График, характеризующий движение изображаюией точки при решении задачи линейного программирования методом Пайна.

grad2=g7./.

Функцию f можно заранее продифференцировать н для производных образовать параллельные моделирующие цепочки. Число этих цепочек

равно числу переменных. При большом числе переменных и сложном нелинейном характере функцив f это не всегда можно практически реализовать.

Если же / квадратичная функция, то производные линейны и относи-

тельно просто реализуются с помощью интегрирующих усилителей.

Обозначая границу области возможных решений через Ф(д:), получаем уравнение для определения k:

откуда

(I к \ grad г + grad Ф, grad Ф) = О, (grad г, grad Ф)

т. е. к в общец случае является функцией дг, что несколько осложняет моделирование. В остальном схема решения подобна линейному случаю.

При решении задач нелинейного программирования число блоков увеличивается сверх 2 (п + т) в связи с необходимостью образования нелинейных

зависимостей и перемножения.

Метод скольжения. При реализации метода скольжения движение изображающей точки внутри области, определенной неравенствами, происходит по направлениям, параллельным координатным осям, т.е. переменные изменяются, так же, как при поиске методом минимизации. Практически это означает, что первый этап движения- движение до границы - может быть осуществлен при решении задач линейного программирования изменением любой одной из переменных в направлении минимума или максимума г. Движение по границе гиперобъема при изменении одной из переменных может быть осуществлено путем определения значений остальных переменных моделированием системы уравнений, определяющей положение этой границы.

Сущность метода скольжения удобнее проследить на примере решения задачи минимизации линейной формы

г = 20 - (Xi -f 2x2)

Xi>0; х>0:

2xi + 32 < 24, .

показанной графически на рис. 5.19.

При подходе к границе, определяемой неравенством 2xi -f < 12, на-iipHMCp в точке А, при изменении переменной должна татъ изменяться также и переменная х, величина которой определяется выражением х = = 12 - Xf. При переходе к новой границе (точка В) изменение переменной должно происходить в соответствии с выражением 2a:i + Зх = 24.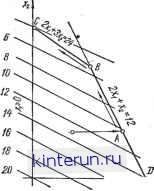

Рис. 5.19. График, характеризующий движение изображающей точки при реализации метода скольжения.

при наличии ограничений